问题: 解决方案
用C#封装一个线程安全的缓存器,达到目标定时更新 错峰缓存,减少数据库IO瓶颈。 using System.Collections.Concurrent; using Tools; namespace SpacePhoneAPI.BackTask { public class CacheManager<T> { private static CacheManager<T>? _instance; private static readonly object LockObject = new …
1.特性定义 [AttributeUsage(AttributeTargets.Property)] public class VerificationAttribute : Attribute { public bool IsEmpty => true; public VerificationAttribute() { } } 2.定义在属性上 /// <summary> /// 域名 /// </summary> [Verification] public string Field…
见代码 [TypeConverter(typeof(DescribedEnumConverter<FlatTypeEnum>))] public enum FlatTypeEnum { [Description("N")] N, [Description("F")] F } public static class EnumExtend<T> where T : Enum { public static T? GetEnumValueByDescription(string desc) { f…
==================================================================== =================================================================== =================================================================== =======================================================…
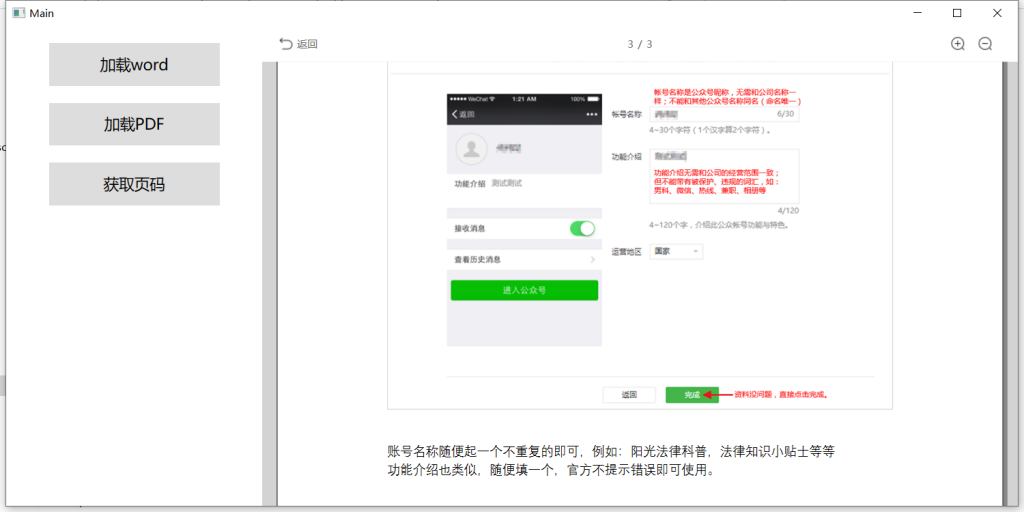
安装完成后: 1.先访问publish页面在线安装插件 2.访问要操作的页面,点击新建客户端打开文件,会自动调起本地的wps并加载test.docx文件
using Spire.Doc; using Spire.Pdf; using System; using System.Collections.Generic; using System.IO; using System.Linq; using System.Text; using System.Threading.Tasks; using System.Windows; using System.Windows.Controls; using System.Windows.Data; using System.…
先nuget搜索安装System.IO.Compression.ZipFile using System; using System.Collections.Generic; using System.IO; using System.Linq; using System.Text; using System.Threading.Tasks; using System.IO.Compression; namespace Build_Exe { public class ZipHelper { /// <sum…
using (FileStream lStream = new FileStream(address, FileMode.Open, FileAccess.Read)) { pic_Image.Image = Image.FromStream(lStream); } 使用上面的方法绑定图片,不会抢占本地加载图片的资源。