首先我们分析下计算概率:
1、52张牌中任意抽三张,排列组合有52*51*50/3*2*1=22100种
2、豹子有 13*4=52种,出现概率0.24%;
3、同花顺有 (13-1)*4=48种,出现概率0.22%;[应为4×11=44种]
4、金花有 4*(13*12*11/6-12)=1096种,出现概率4.96%;[应为4×(13×12×11/3!-11)=1100种]
5、顺子有 (4*4*4-4)*12=720种,出现概率3.26%;[应为11×4^3-44=660种]
6、对子有 4*3/2*12*4*13=3744种,出现概率16.94%;[应为13×(4×3/2!)×50-52=3848种]
7、单张有22100-52-48-1096-720-3744=16440种,出现概率73.49%;
散牌中,A最大的统称单A,计算方法是:
单A12*11/2*4*4*4-4*12*11/2-2*4*4*4+2*4=3840;
单K 11*10/2*4*4*4-4*11*10/2-4*4*4+4=3240;
单Q 10*9/2*4*4*4-4*10*9/2-4*4*4+4 =2640;
单J 9*8/2*4*4*4-4*9*8/2-4*4*4+4 =2100;
单10 8*7/2*4*4*4-4*8*7/2-4*4*4+4 =1620;
依此类推计算。 分析:由以上统计不难看出,同花顺出现的概率比豹子要小,顺子出现的概率比金花要小。也就是我们常用的大小尺度有不合理的地方。 拿到对儿以上就很不错了(25.61%);拿了顺子以上的牌,就更不容易了(8.67%),以下是玩牌的人数与出大牌的概率对比;
人数 每局有顺以上大牌出现的概率
1 8.67%
9 55.79%
2 16.59%
10 59.62%
3 23.82%
11 63.12%
4 30.42%
12 66.32%
5 36.46%
13 69.24%
6 41.97%
14 71.91%
7 47.00%
15 74.34%
8 51.59%
16 76.57%
“人多出大牌”就是这个道理。
然后简单说下我这里的做法:
一共可能性是22100种,对于计算机来说这个量很小,所以我初始化的时候,先枚举出所有可能性,并且给他们定下点数大小的score。
随机发牌,然后根据当前牌的大小判断它的位置,然后在加上人数做为参数,计算出胜率,败率和平率。
我在计算中,排除了已知的3张手牌
计算方法代码如下:
string probability = (Math.Abs(1 - Math.Pow((1 - count / CardFlowerList.Count), manCount)) * 100).ToString("N2") + "%";
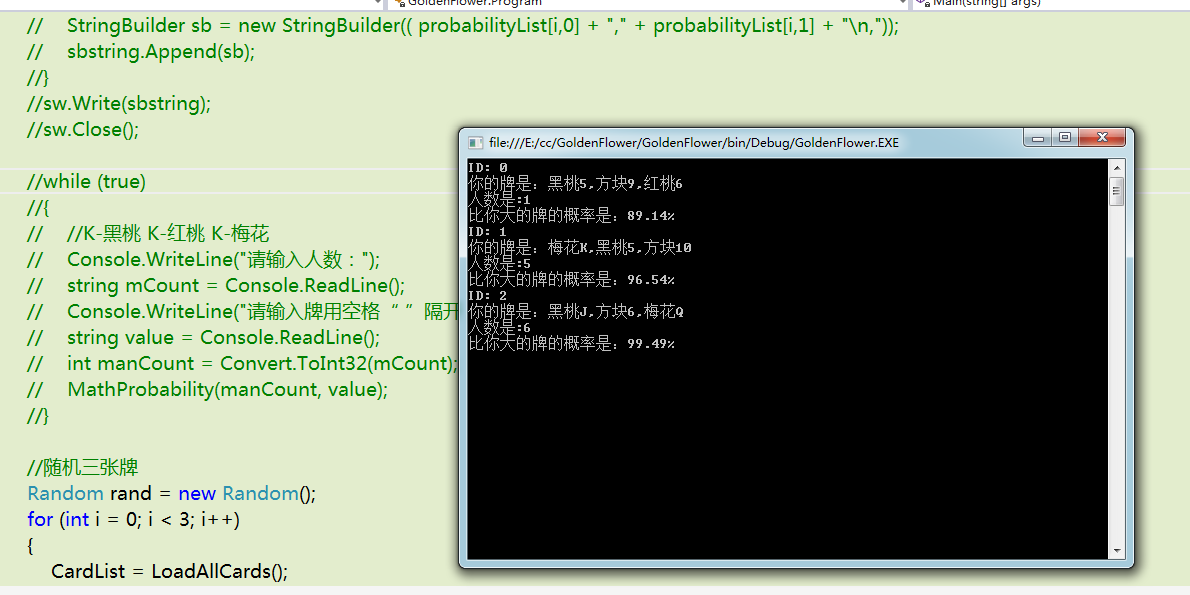
Console.WriteLine("你的牌是:" + myCards[0].CardColor + myCards[0].Name + "," + myCards[1].CardColor + myCards[1].Name + ","
+ myCards[2].CardColor + myCards[2].Name);
Console.WriteLine("人数是:" + manCount);
Console.WriteLine("比你大的牌的概率是:" + probability);
排列大小的源码:
/// <summary>
/// 大小
/// </summary>
/// <param name="cards"></param>
/// <param name="type"></param>
/// <returns></returns>
public static int GetLevel(List<Card> cards, Type type)
{
List<int> level = cards.Select(s => s.Level).ToList();
level.Sort();
switch (type.TypeLevel)
{
case 1://豹子 13
return 15 - cards[0].Level;
case 2://同花顺 12 A23,234,345,456,567,678,789,890,90j,0jq,jqk,qkA
int baseLevel = 14;
if (level[2] == 14 && level[1] == 3)
{
return 25;//A23
}
else
{
int mLevel = baseLevel + (14 - level[2]);
return mLevel;
}
case 3://同花 274
int tbaseLevel = 26;
int value = 0;
for (int i = 14; i > 4; i--)
{
for (int j = i - 1; j > 2; j--)
{
for (int n = j - 1; n > 1; n--)
{
List<Card> cardLs = new List<Card>();
Card c = new Card();
c.Level = i;
cardLs.Add(c);
Card c2 = new Card();
c2.Level = j;
cardLs.Add(c2);
Card c3 = new Card();
c3.Level = n;
cardLs.Add(c3);
if (IsList(cardLs))
continue;
else
{
if (level[2] == i && level[1] == j && level[0] == n)
{
int mLevel = tbaseLevel + value;
return mLevel;
}
value++;
}
}
}
}
break;
case 4://顺子 12
int baseSLevel = 300;//274+12+13+1
if (level[2] == 14 && level[1] == 3)
{
return 311;//A23
}
else
{
int mLevel = baseSLevel + (14 - level[2]);
return mLevel;
}
case 5://对子 13*12=156
int baseDLevel = 312;
int dLevel = 0;
for (int i = 14; i > 1; i--)
{
for (int j = 14; j > 1; j--)
{
int mLevel = baseDLevel + dLevel;
if ((level[0] == i && level[1] == i && level[2] == j) ||
(level[1] == i && level[2] == i && level[0] == j))
{
dLevel++;
return mLevel;
}
}
}
break;
case 6://杂牌 274
int baseZLevel = 468;
int zValue = 0;
for (int i = 14; i > 4; i--)
{
for (int j = i - 1; j > 2; j--)
{
for (int n = j - 1; n > 1; n--)
{
List<Card> cardLs = new List<Card>();
Card c = new Card();
c.Level = i;
cardLs.Add(c);
Card c2 = new Card();
c2.Level = j;
cardLs.Add(c2);
Card c3 = new Card();
c3.Level = n;
cardLs.Add(c3);
if (IsList(cardLs))
continue;
else
{
if (level[2] == i && level[1] == j && level[0] == n)
{
int mLevel = baseZLevel + zValue;
return mLevel;
}
zValue++;
}
}
}
}
break;
}
return 0;
}
文章评论